In his e book The Mathematical Universe, mathematician William Dunham wrote of John Venn’s namesake legacy, the Venn diagram, “No one in the long history of mathematics ever became better known for less.” Whereas Venn diagrams might not have solved any long-standing open issues, certainly these interlocking rings deserve extra credit score. Their compact illustration of group relationships explains their enduring enchantment in school rooms, infographics and Web memes.
Not merely visible aids, Venn diagrams may help us clear up on a regular basis logic issues, and so they give rise to shocking geometric questions. Have you ever ever seen a correct Venn diagram with 4 overlapping circles? No, as a result of it’s not possible. Venn himself found this and got here up with a intelligent repair, however this solely begot deeper geometric puzzles that mathematicians nonetheless research right now.
Venn debuted his diagrams in 1880 as a way for visualizing modern advances in logic. They then discovered utility within the intently associated department of math known as set principle, which focuses on collections of objects. Venn diagrams usually include overlapping circles, with every representing some set of components, (e.g., issues which are cuddly or Broadway exhibits). The overlapping area between two circles incorporates components that belong to each units (e.g., “cats”). Very similar to in utilizing scatter plots in statistics or drawing shapes in geometry, seeing one’s drawback typically clarifies it.
On supporting science journalism
In case you’re having fun with this text, contemplate supporting our award-winning journalism by subscribing. By buying a subscription you might be serving to to make sure the way forward for impactful tales in regards to the discoveries and concepts shaping our world right now.
Think about you’re planning a cocktail party and navigating your folks’ fickle preferences. If Wilma attends, then so will Fred. If Barney attends, then so will any individual else. Barney received’t come if Wilma comes, however he’ll if she doesn’t. If Fred and Barney each attend, then so will Wilma. Who must you count on to point out up? This poser is tough to work via after we are solely given the textual content. A Venn diagram offers a scientific strategy to visualize and clear up it. Every assertion precludes some potential outcomes, which we point out by shading the corresponding areas of the Venn diagram.
Most Venn diagrams you encounter depict both two or three overlapping circles, however what when you have 4 or extra units to think about?
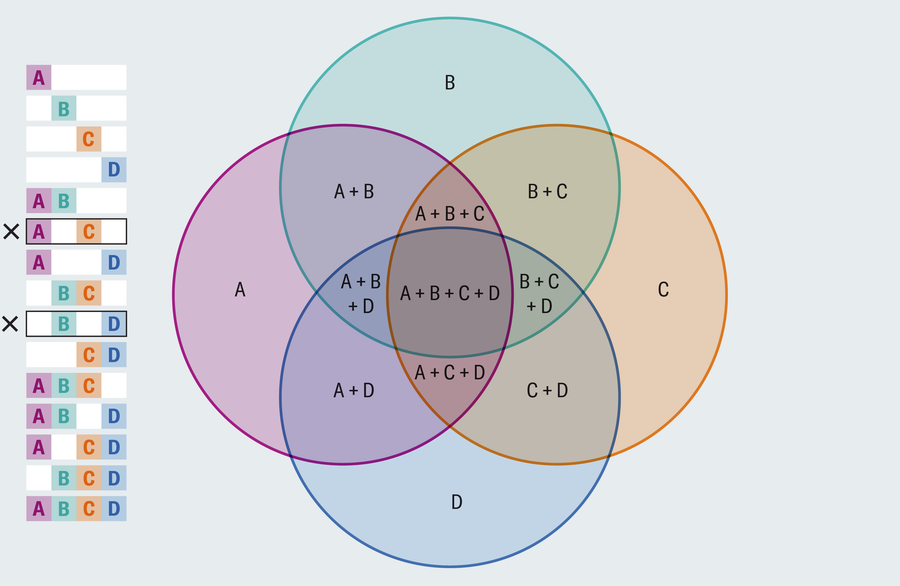
Did you notice the issue? There is no such thing as a area the place solely A and C overlap that doesn’t additionally embody one other area, and likewise for B and D. A correct Venn diagram depicts each mixture of intersections. Rejiggering the format received’t assist. Each four-circle drawing suffers the identical flaw.
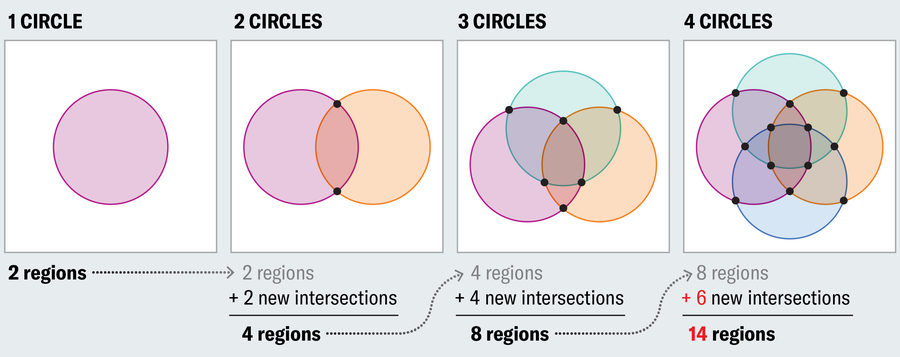
To see why, begin with a single circle and observe that it establishes two areas—inside and exterior. After we add a second set of components (a brand new circle), we double the probabilities, so we have to double the variety of areas (first set, second set, each units and neither set). The one method to do that is to have the second circle intersect the primary at two factors (touching at just one level would lead to solely three areas: first set, second set or neither). This pattern continues, the place every new circle should double the variety of areas if we wish to symbolize all logical potentialities. However the variety of new areas can’t exceed the variety of new intersections, and a brand new circle can intersect the present circles at solely two factors every. This works high quality when including a 3rd circle as a result of we have to add 4 areas, and the brand new circle can intersect the 2 current circles at two factors every for 4 whole new intersection factors. However it breaks down with a fourth circle, the place we’d like eight new areas however can solely muster six new factors of intersection.
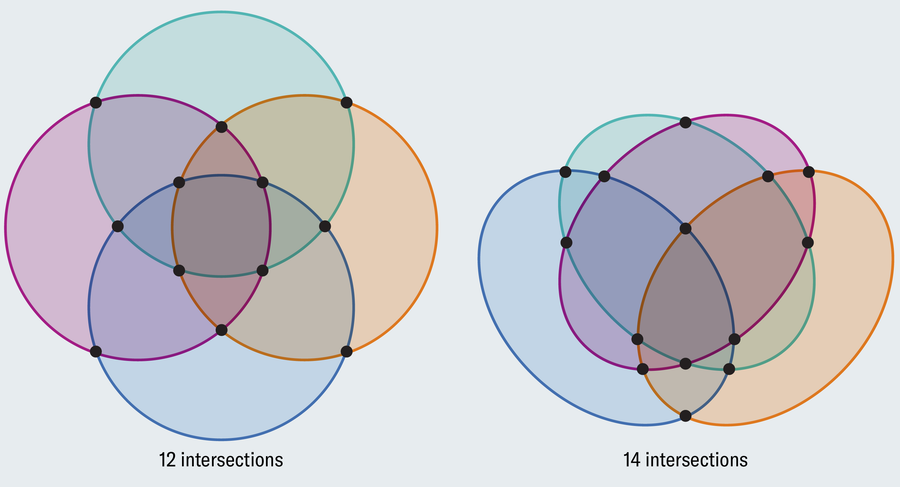
After all, we don’t want to limit ourselves to circles. We may simply hint a wiggly loop via a three-circle diagram in order that it carves out the required variety of areas, however we’d lose the class within the diagram. 4 intersecting spheres may symbolize the suitable variety of areas, however three-dimensional visuals are exhausting to parse. John Venn knew of the shortcoming with circles, so he proposed ellipses to symbolize 4 units.
Amanda Montañez; Supply: “Venn Diagrams and Independent Families of Sets,” by Branko Grünbaum in Arithmetic Journal, Vol. 48, No. 1; January 1975 (reference)
Not like circles, two ellipses can intersect at 4 factors. This overcomes the restrictions with circles however solely briefly. Ellipses work for 4 and 5 units earlier than failing in the identical method that circles did. Because the variety of units grows, we’d like increasingly more unique shapes to painting them.
One may moderately argue that past 4 units of components, Venn diagrams lose their utility. The four-ellipse picture is already fairly chaotic. Perhaps for five-plus units we should always abandon visible representations. However utility doesn’t animate the mathematician a lot as magnificence and curiosity. Though Venn diagrams initially utilized to logic and set principle, the four-circle conundrum raised an fascinating geometry query. That seed has blossomed into an enchanting investigation into the geometry of Venn diagrams that continues right now.
Venn and his successors believed that ellipses couldn’t painting all 32 areas required for a five-set diagram. Not till 1975 did mathematician Branko Grünbaum show them incorrect by instance:

Amanda Montañez; Supply: “Venn Diagrams and Independent Families of Sets,” by Branko Grünbaum in Arithmetic Journal, Vol. 48, No. 1; January 1975 (reference)
Discover additionally that Grünbaum’s diagram shows a lovely rotational symmetry. Spinning it one fifth of a full rotation lands it again on itself, leaving the unique form unchanged. Typical two- and three-circle Venn diagrams share this property. Rotate a two-circle Venn diagram by 180 levels (or a three-circle one by 120 levels), and it seems to be the identical. However the four-ellipse diagram doesn’t have rotational symmetry. Can that be mounted? What do two, three and 5 have in frequent that 4 doesn’t?
In 1960 a then undergraduate pupil at Swarthmore School, David W. Henderson, answered this query with a shocking discovery (Stan Wagon and Peter Webb stuffed in some gaps later): Rotationally symmetric Venn diagrams are potential solely when the variety of units is a prime quantity—a quantity divisible solely by 1 and itself, resembling 2, 3 and 5 however not 4. Henderson solely confirmed {that a} prime variety of units is critical, not which you could all the time design a symmetric Venn diagram for each prime quantity. Thus started a contest to search out bigger and bigger examples. Right here’s a wild-looking 11-set Venn diagram from Peter Hamburger.
Mathematicians on the College of South Carolina settled the query in 2004 by exhibiting that rotationally symmetric Venn diagrams exist for each prime variety of units. In case you assume this prompted mathematicians to pack up their pencils and lay the research of Venn diagrams to relaxation, you then haven’t been following alongside. As a substitute the group has raised their aesthetic requirements, searching for figures with even extra refined properties.
Our opening quote contended that Venn diagrams are overrated. Even those that agree should admit that they’ve a curious attract. Take the units of fascinating matters in logic, in geometry and in visualization, and also you’ll discover Venn diagrams on the intersection.

