To mathematicians, equations are artwork. Simply as many are moved by a portray or piece of music, to those that recognize and perceive math, expressions of numbers, variables, operations and relations between portions might be simply as compelling.
As is the case with inventive magnificence, mathematical magnificence is within the eye of the beholder. One mathematician might prize simple-to-state, succinct equations, whereas one other might favor the alternative. And simply as some favor trendy artwork whereas others desire medieval works, each historical and modern equations are admired for his or her cleverness, energy and risk.
Listed here are some mathematicians’ picks of probably the most stunning math equations, in addition to their very own phrases on what components make them so beautiful.
On supporting science journalism
For those who’re having fun with this text, contemplate supporting our award-winning journalism by subscribing. By buying a subscription you’re serving to to make sure the way forward for impactful tales concerning the discoveries and concepts shaping our world in the present day.
Loewner Differential Equation
Some equations are stunning as a result of they reveal surprising relationships between totally different topics. The Loewner differential equation, launched by Charles Loewner in 1923, describes the time evolution of a household of conformal (angle-preserving) features outlined on subsets of the complicated airplane. The enter for the equation is a steady perform W(t), known as the driving perform.
Practically 80 years later, in 1999, Oded Schramm found that the answer to the Loewner equation has particular symmetries when the driving perform is taken to be Brownian movement, a random perform that may be a central object of examine in likelihood principle. Constructing on Schramm’s discovery, it was confirmed that the answer to the Loewner equation for this selection of driving perform, known as Schramm-Loewner evolution, describes the large-scale habits of assorted important fashions in two-dimensional statistical mechanics. This utility of the Loewner equation in likelihood principle was fully surprising previous to Schramm’s work. It revolutionized the mathematical examine of statistical mechanics and has led to among the most enjoyable breakthroughs in arithmetic prior to now 20 years. —Ewain Gwynne, College of Chicago
Gauss-Bonnet Equation
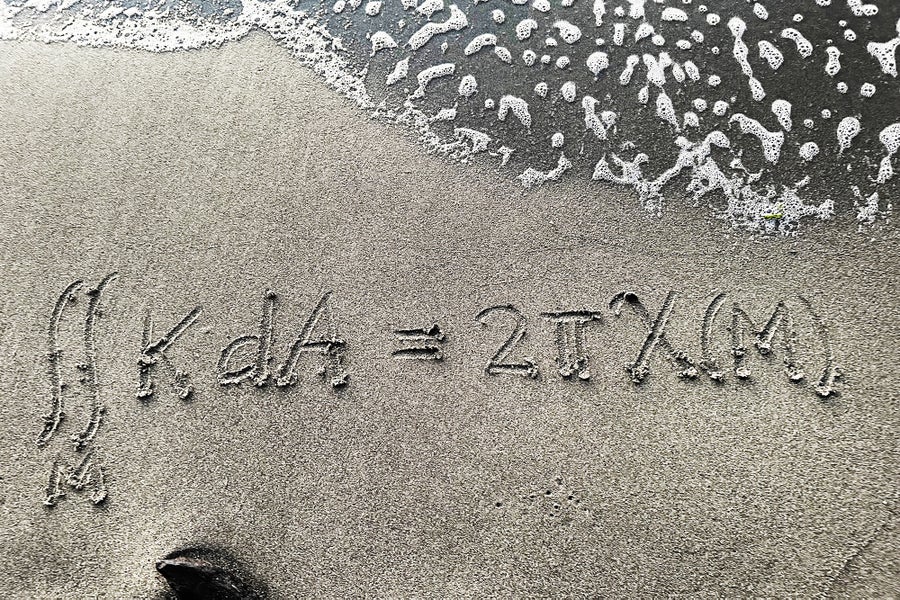
The Gauss-Bonnet system is a good looking equation in differential geometry that asserts the equality of the integral of the Gauss curvature over a floor and a continuing multiplied by the Euler attribute of the floor. The equation is outstanding as a result of it relates two very totally different portions: the curvature of the floor on the one hand and the topology of the floor then again. The curvature of a floor at some extent is a measure of the bending of the floor at that time, or how a lot the floor deviates from being a airplane. The Euler attribute is a world topological invariant of the floor that describes the topological construction of the floor no matter how it’s bent. The equation is stunning as a result of, for instance, it implies that if you happen to constantly deform a floor, the overall curvature will stay unchanged. Variations of the Gauss-Bonnet equation had been first formulated by Carl Friedrich Gauss and Pierre Ossian Bonnet within the first half of the nineteenth century, and it stays one of the vital stunning and putting equations in geometry. Some stunning points of this equation are the simplicity of its expression and the profoundness of what it says. —Ailana Fraser, College of British Columbia
Sobolev Inequality
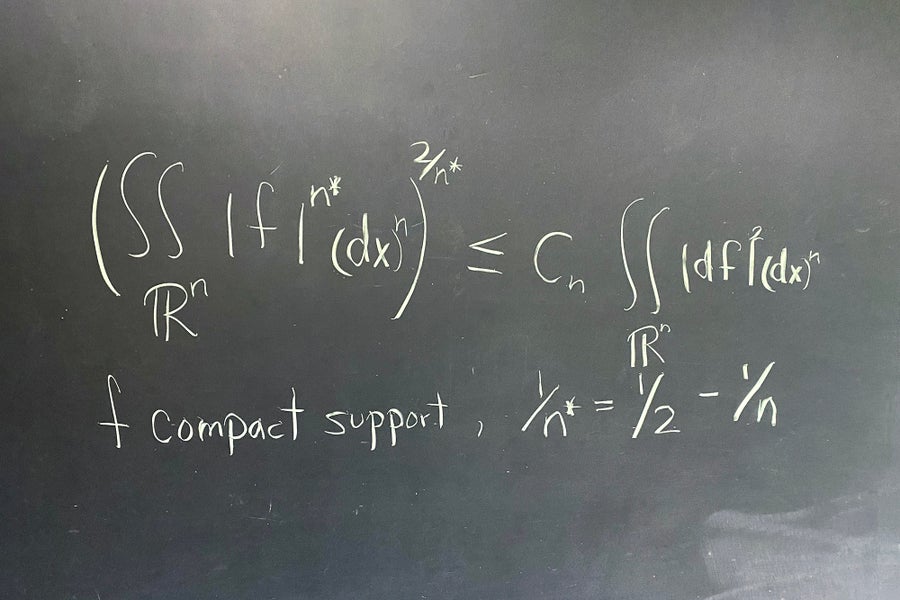
I like inequalities. The Sobolev and associated inequalities estimate features by way of derivatives and type the premise for our understanding of partial differential equations. The failure of the inequality for n = 2 pertains to properties particular to n = 2. —Karen Uhlenbeck, College of Texas at Austin
Riemann-Roch Equality
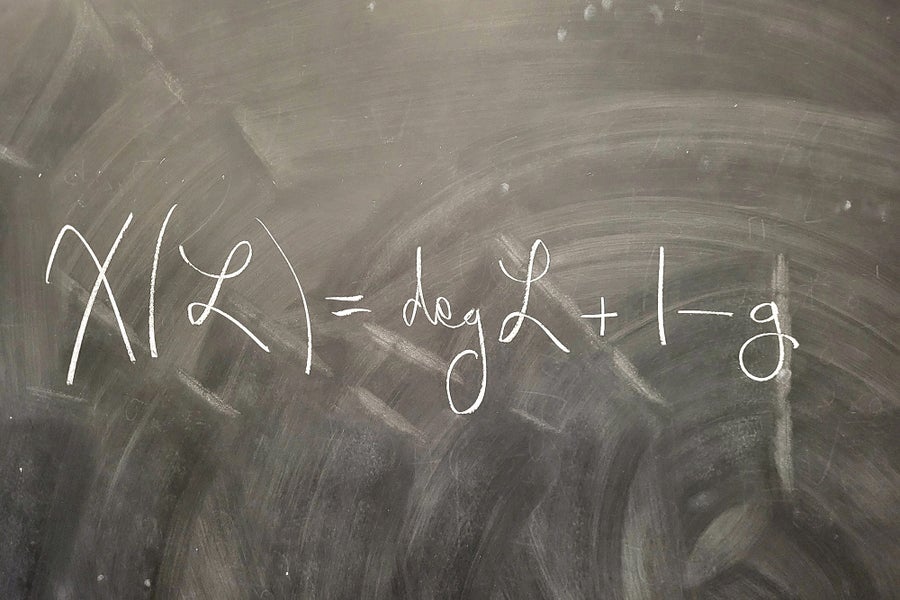
A Riemann floor is a compact orientable floor. Riemann surfaces are distinguished by the variety of holes or handles they admit. This quantity is known as the genus, and it’s denoted by g. As an example, a Riemann floor of g=0 is a sphere, and a Riemann floor of g=1 is a torus, or doughnut. A posh Riemann floor is a Riemann floor with a fancy construction on it. In different phrases, it’s also a fancy manifold.
A divisor on a Riemann floor is a selection of finitely many factors. The diploma of a divisor is the variety of factors in it. It’s denoted by “deg.” A priori, a divisor relies upon merely on topological data, as does the diploma of the divisor. As soon as a Riemann floor is supplied with a fancy construction, nonetheless—in different phrases, when it’s thought-about a fancy manifold—then one might ask questions on that complicated construction, akin to whether or not there’s a meromorphic perform whose zeros or poles agree with a given divisor. This results in a model of the classical Mittag-Leffler drawback. One of many easiest invariants which can be decided by the complicated construction is the holomorphic Euler attribute of a divisor, which, in a method, is a correction time period for the Mittag-Leffler drawback on this specific Riemann floor. For a divisor ℒ, its holomorphic Euler attribute is denoted by χ(ℒ).
Now we’re able to state the Riemann-Roch equality. Contemplate a fancy Riemann floor of genus g and a divisor ℒ on it. The equation is χ(ℒ) = degℒ + 1 – g.
This easy-looking equation has far-reaching penalties. Amongst different issues, it implies that the holomorphic Euler attribute solely depends upon topological data.
As for what makes an equation stunning, I’d say that those I discover intriguing are those who both reveal one thing surprising or join seemingly unrelated invariants. —Sándor Kovács, College of Washington
Isomorphism between Graded Rings

I discover this equation stunning as a result of it’s novel and stunning, and knowledge clearly flows from the right-hand time period (RHT) to the left-hand time period (LHT). Certainly, the LHT is manifestly geometric, whereas the RHT is only algebraic. Moreover, as a result of the RHT is calculable, this equation provides a classification of manifolds, an enterprise of intense examine. Lastly, this end result was a primary of its sort, whose proof methods prompted inventive new approaches to and views in lots of areas of math. —David Ayala, Montana State College
An Infinite Sum
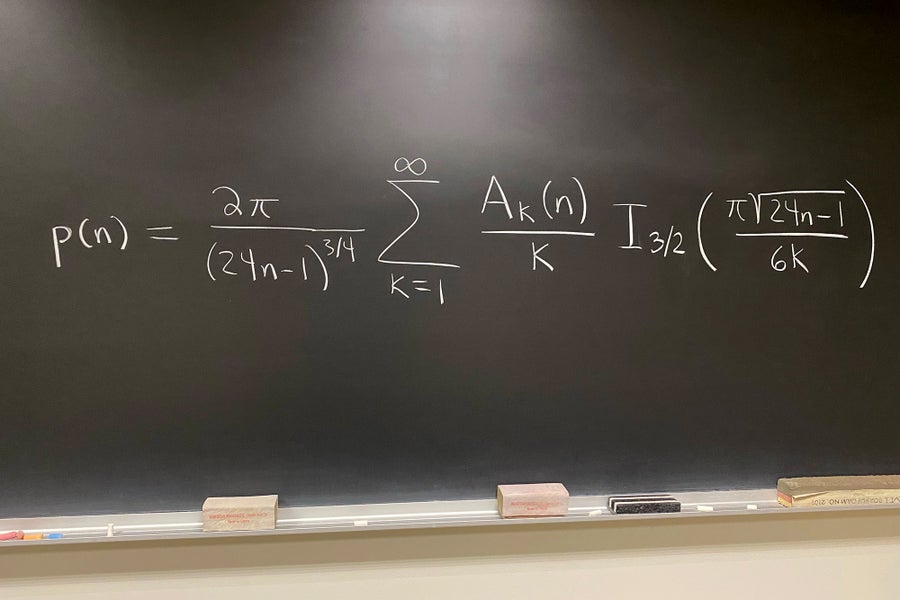
I don’t suppose there’s a single most stunning mathematical equation, however this one stands out to me. I confirmed {a photograph} of it to a younger baby whereas engaged on this piece. We first talked about what an equation is (a mathematical assertion relating two issues with an equals signal, akin to 4 = 2 + 1 + 1), they usually requested why this equation is so huge. We talked about how the right-hand aspect is visually the large aspect however the left-hand aspect isn’t—how the right-hand aspect is a sum (like 2 + 1 + 1) however of an infinite variety of phrases and the way the left-hand aspect has to do with integer partitions in quantity principle. For instance, there are 5 partitions of n = 4 (4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1), so the partition perform p(n) evaluated at n = 4 is 5 (p(4) = 5).
This essential and seemingly fundamental perform having to do with including and counting is superbly and maybe unexpectedly complicated. For instance, p(100) is greater than 190 million, however certainly the way in which to determine that out isn’t by writing out the hundreds of thousands of partitions of n = 100 and counting what number of there are. The proper-hand aspect of this equation is an actual system for p(n) because of the 1937 work of Hans Rademacher, who prolonged associated earlier work of G. H. Hardy and Srinivasa Ramanujan. Some might view the (huge) right-hand aspect, an infinite sum involving sums of complicated (imaginary) numbers (Aok(n)), fractional powers (3/4 and the sq. root), the transcendental quantity pi, and extra, as the alternative of gorgeous or as intimidating—particularly provided that it replaces the (visually small) left-hand aspect that even a baby can perceive. It’s the fantastic thing about analytic quantity principle and Rademacher and Hardy and Ramanujan’s work that exhibits that this system for p(n) exists—a feat in and of itself—and that it seems to be sensible for computing p(n) by truncating the infinite sum and basically rounding. It’s stunning that the infinite sum that seems right here converges, which means it sums to one thing finite, an actual quantity that counts one thing of significance, and doesn’t carry on accumulating—to not point out the mathematical legacy, additional analysis and connections to different areas that persist in the present day, now near a century later. —Amanda Folsom, Amherst School
The Euler Product Components
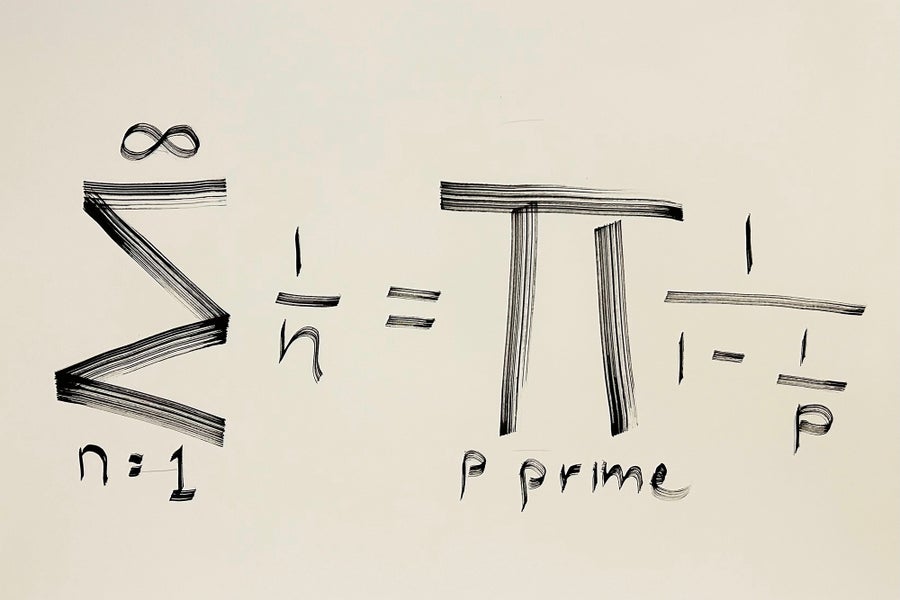
It’s laborious to choose a single most stunning equation in arithmetic, however I believe that the Euler product system can be close to the highest of any such listing. Let me extol the virtues of this system. First, it’s easy. It solely includes the operations of addition, subtraction, multiplication and division. Second, it’s basic: it expresses a deep relationship between counting numbers on the left-hand aspect and prime numbers on the right-hand aspect. Third, it’s stunning and surprising, intertwining the fundamental operations in a really novel method. Fourth, it’s helpful and highly effective. Simply as a begin, it provides one other proof of the infinitude of primes. The left-hand aspect is a divergent sequence. If there have been solely finitely many primes, the right-hand aspect can be finite, a contradiction. One can even squeeze deeper details about primes from the equation. As an example, one can use the Euler product system to show that the sum of the reciprocals of the primes diverges. This can be a end result that goes method past Euclid’s basic proof of the infinitude of primes. Fifth, the system is completely present. It nonetheless performs a significant position in quantity principle and is among the key instruments in understanding the distribution of prime numbers, even to today. Sixth, it’s accessible: it has a chic proof that makes use of the truth that integers might be uniquely factored, together with neat properties of geometric sequence. —Richard Schwartz, Brown College
A Reifenberg FlatSet
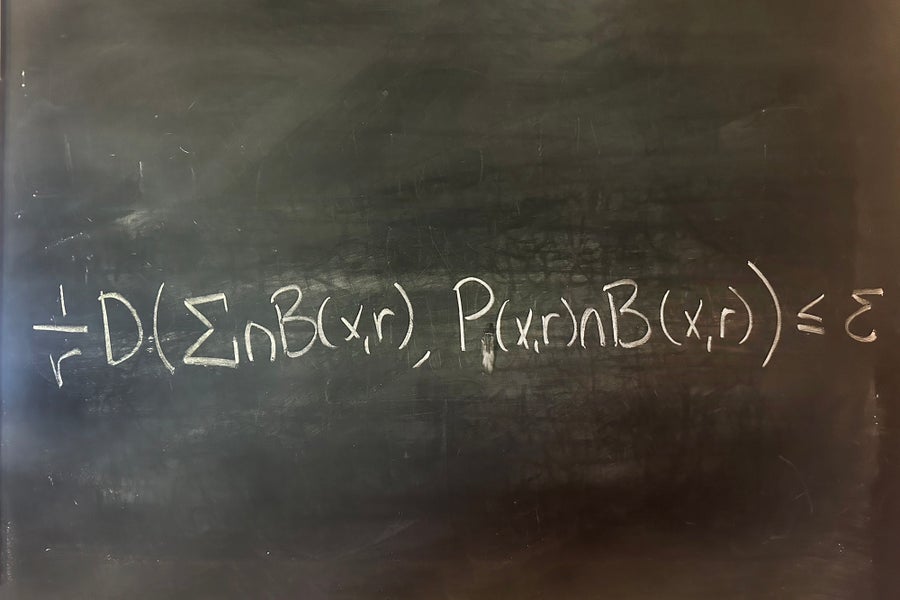
A set Σ whose factors fulfill the inequalities within the image (they’re hidden, however there are two!) is known as Reifenberg flat. As typical, the image ε in arithmetic represents a small amount; we’re basically saying that in each ball B(x,r), at each scale and location, there exists a airplane P(x,r), whose distance from our set could be very tiny (εr).
Peter Reifenberg proved in 1960 that topologically, these units are disks. (That’s a great factor: no rips, holes or bizarre twists.) Actually, as more moderen outcomes present, asking these units to be slightly further flat results in smoother parameterizations. Being flat is kind of demanding for a set, but it surely certain pays off in regularity. The interaction between flatness (geometry) and regularity (evaluation) is on the coronary heart of all the pieces I like about math, and it’s one thing that almost all readers already know however might not understand: we study early on that derivatives give us tangents!
I don’t suppose that the sweetness in arithmetic lies within the equations, though I’m sure that good handwriting could make miracles. I overwhelmingly discover it within the concepts which can be able to bringing two mathematical universes collectively to create room for brand spanking new ideas whereas enhancing our understanding of previous ones. —Silvia Ghinassi, College of Washington
(1/p) + (1/q) + (1/r) = 1
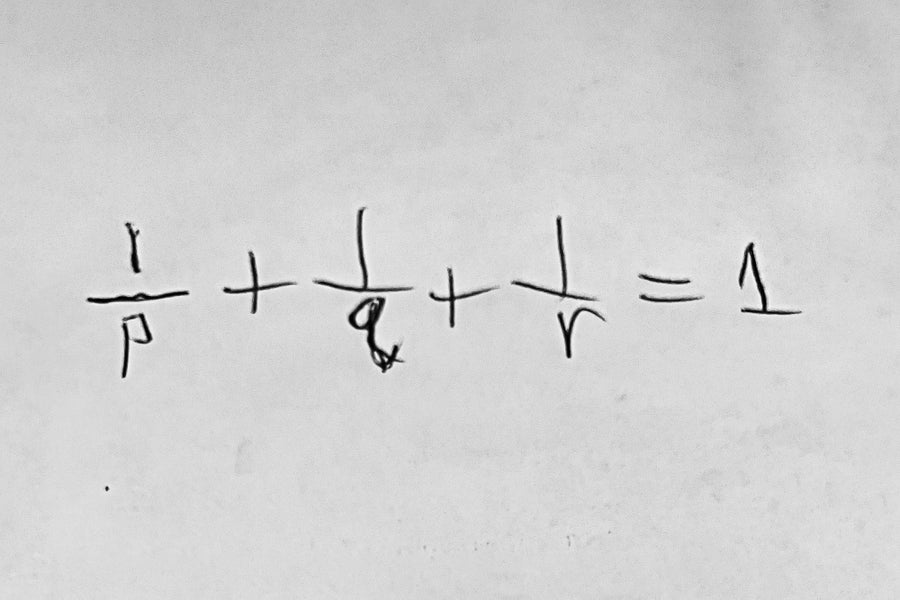
My favourite equation is (1/p) + (1/q) + (1/r) = 1. Its solely options in constructive integers are p = q = r = 3; p = 2, q = r = 4; and p = 2, q = 3, r = 6. This equation pertains to a good looking class of teams known as Coxeter, or reflection, teams and marks the essential boundary between finite and infinite teams of this sort. Its options are intimately associated to the one methods of tiling the airplane by common polygons, specifically by equilateral triangles, squares or hexagons. —Monty McGovern, College of Washington

