French mathematician Édouard Lucas was born in Amiens in 1842 and died in Paris 49 years later. He wrote the four-volume work Recréations Mathématiques, which turned a basic of leisure arithmetic. In 1883, below the pseudonym “N. Claus de Siam” (an anagram of “Lucas d’Amiens”), he marketed a solitaire recreation that he known as the Tower of Hanoi.
He claimed that the sport was a simplified model of the so-called Tower of Brahma. On this supposed legend, monks needed to transfer a tower made from 64 golden disks in a terrific temple. Earlier than they may full this process, nonetheless, the temple would crumble to mud, and the top of the world would arrive.
The Tower of Hanoi consists of a small board on which three an identical cylindrical rods are mounted. On the left rod there are 5 disks of various sizes with a gap within the center. They’re ordered by dimension, with the biggest disk on the backside. The purpose of the sport is to maneuver all of the disks from the left rod to the appropriate rod in as few strikes as doable. In every transfer, just one disk might be taken from one rod and positioned on one other rod, and a bigger disk can by no means be positioned on a smaller disk. What number of and which strikes are mandatory to move the disks?
We change the disks with numbers based on dimension. Now we construct the answer systematically, beginning with a tower with just one disk. The answer is trivial. With one transfer you transport the only disk from left to proper.

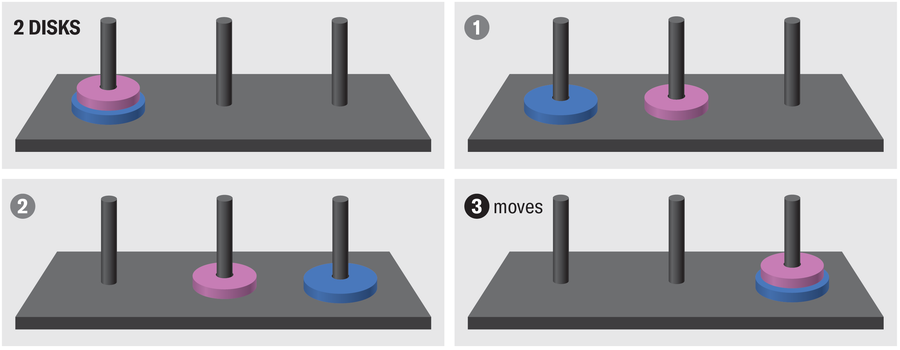
For a tower with two disks you first transfer disk 1 from left to center, then disk 2 from left to proper and eventually disk 1 from center to proper. So that you want 3 = 22 – 1 strikes.
For a tower with three disks we first mentally depart disk 3 out. This reduces the issue to the duty with solely two disks, which we now transport from left to center with three strikes. With a fourth transfer we then transport disk 3 three from left to proper. Now we mentally depart disk 3 out time and again transport the 2 disks from center to proper with three strikes. In whole this consists of three + 1 + 3 = 7 = 23 – 1 strikes.

The issue of the tower with 4 disks might be decreased in a really analogous option to that of the tower with three disks. Due to this fact, you want 7 + 1 + 7 = 15 = 24 – 1 strikes. Lastly, for the tower with 5 disks, you want 15 + 1 + 15 = 31 = 25 – 1 strikes. Basically, you want 2n – 1 strikes for a tower with n disks. The unique recreation by Édouard Lucas had eight disks.
We’d love to listen to from you! E-mail us at video games@sciam.com to share your expertise.
This puzzle initially appeared in Spektrum der Wissenschaft and was reproduced with permission.

