Picture by Editor | Midjourney
Bayesian considering is a approach to make choices utilizing likelihood. It begins with preliminary beliefs (priors) and adjustments them when new proof is available in (posterior). This helps in making higher predictions and choices primarily based on knowledge. It’s essential in fields like AI and statistics the place correct reasoning is necessary.
Fundamentals of Bayesian Concept
Key phrases
- Prior Chance (Prior): Represents the preliminary perception concerning the speculation.
- Probability: Measures how properly the speculation explains the proof.
- Posterior Chance (Posterior): Combines the prior likelihood and the probability.
- Proof: Updates the likelihood of the speculation.
Bayes’ Theorem
This theorem describes the right way to replace the likelihood of a speculation primarily based on new data. It’s mathematically expressed as:
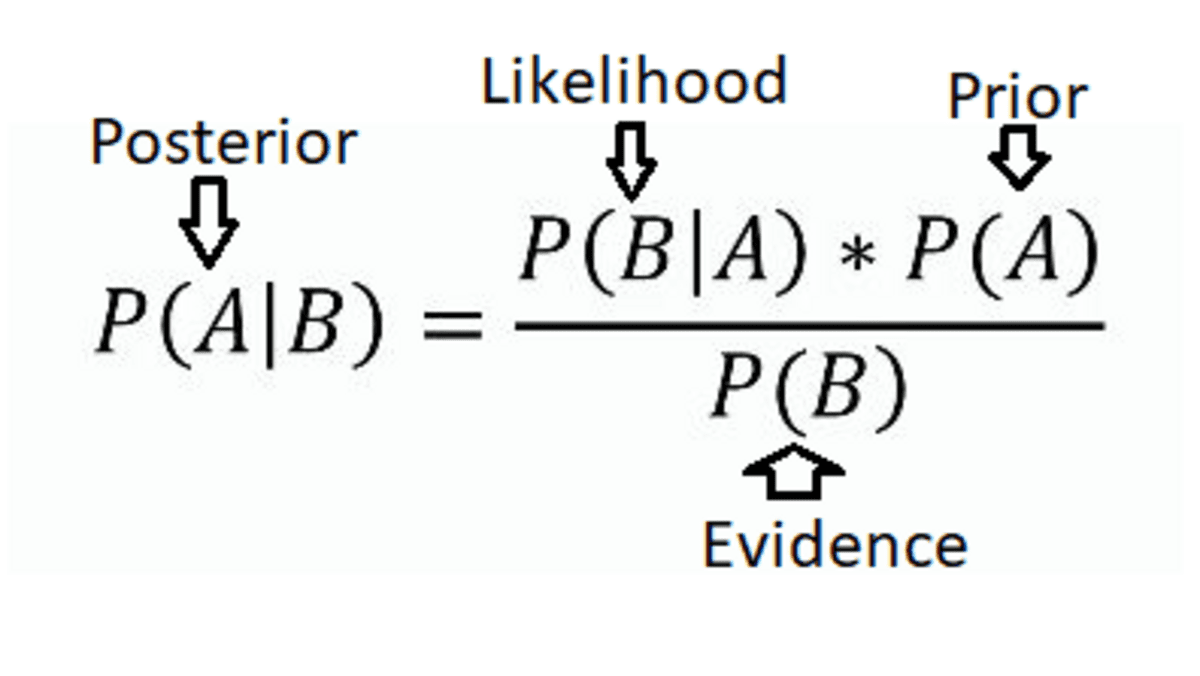 Bayes’ Theorem (Supply: Eric Castellanos Weblog)
Bayes’ Theorem (Supply: Eric Castellanos Weblog)the place:
P(A|B) is the posterior likelihood of the speculation.
P(B|A) is he probability of the proof given the speculation.
P(A) is the prior likelihood of the speculation.
P(B) is the overall likelihood of the proof.
Purposes of Bayesian Strategies in Information Science
Bayesian Inference
Bayesian inference updates beliefs when issues are unsure. It makes use of Bayes’ theorem to regulate preliminary beliefs primarily based on new data. This strategy combines what’s identified earlier than with new knowledge successfully. This strategy quantifies uncertainty and adjusts possibilities accordingly. On this method, it repeatedly improves predictions and understanding as extra proof is gathered. It’s helpful in decision-making the place uncertainty must be managed successfully.
Instance: In medical trials, Bayesian strategies estimate the effectiveness of latest therapies. They mix prior beliefs from previous research or with present knowledge. This updates the likelihood of how properly the remedy works. Researchers can then make higher choices utilizing previous and new data.
Predictive Modeling and Uncertainty Quantification
Predictive modeling and uncertainty quantification contain making predictions and understanding how assured we’re in these predictions. It makes use of strategies like Bayesian strategies to account for uncertainty and supply probabilistic forecasts. Bayesian modeling is efficient for predictions as a result of it manages uncertainty. It doesn’t simply predict outcomes but in addition signifies our confidence in these predictions. That is achieved by posterior distributions, which quantify uncertainty.
Instance: Bayesian regression predicts inventory costs by providing a variety of attainable costs quite than a single prediction. Merchants use this vary to keep away from threat and make funding selections.
Bayesian Neural Networks
Bayesian neural networks (BNNs) are neural networks that present probabilistic outputs. They provide predictions together with measures of uncertainty. As an alternative of mounted parameters, BNNs use likelihood distributions for weights and biases. This enables BNNs to seize and propagate uncertainty by the community. They’re helpful for duties requiring uncertainty measurement and decision-making. They’re utilized in classification and regression.
Instance: In fraud detection, Bayesian networks analyze relationships between variables like transaction historical past and consumer habits to identify uncommon patterns linked to fraud. They enhance the accuracy of fraud detection techniques as in comparison with conventional approaches.
Instruments and Libraries for Bayesian Evaluation
A number of instruments and libraries can be found to implement Bayesian strategies successfully. Let’s get to learn about some in style instruments.
PyMC4
It’s a library for probabilistic programming in Python. It helps with Bayesian modeling and inference. It builds on the strengths of its predecessor, PyMC3. It introduces vital enhancements by its integration with JAX. JAX provides computerized differentiation and GPU acceleration. This makes Bayesian fashions quicker and extra scalable.
Stan
A probabilistic programming language carried out in C++ and accessible by numerous interfaces (RStan, PyStan, CmdStan, and so forth.). Stan excels in effectively performing HMC and NUTS sampling and is thought for its pace and accuracy. It additionally contains in depth diagnostics and instruments for mannequin checking.
TensorFlow Chance
It’s a library for probabilistic reasoning and statistical evaluation in TensorFlow. TFP supplies a variety of distributions, bijectors, and MCMC algorithms. Its integration with TensorFlow ensures environment friendly execution on numerous {hardware}. It permits customers to seamlessly mix probabilistic fashions with deep studying architectures. This text helps in sturdy and data-driven decision-making.
Let’s take a look at an instance of Bayesian Statistics utilizing PyMC4. We are going to see the right way to implement Bayesian linear regression.
import pymc as pm
import numpy as np
# Generate artificial knowledge
np.random.seed(42)
X = np.linspace(0, 1, 100)
true_intercept = 1
true_slope = 2
y = true_intercept + true_slope * X + np.random.regular(scale=0.5, dimension=len(X))
# Outline the mannequin
with pm.Mannequin() as mannequin:
# Priors for unknown mannequin parameters
intercept = pm.Regular("intercept", mu=0, sigma=10)
slope = pm.Regular("slope", mu=0, sigma=10)
sigma = pm.HalfNormal("sigma", sigma=1)
# Probability (sampling distribution) of observations
mu = intercept + slope * X
probability = pm.Regular("y", mu=mu, sigma=sigma, noticed=y)
# Inference
hint = pm.pattern(2000, return_inferencedata=True)
# Summarize the outcomes
print(pm.abstract(hint))
Now, let’s perceive the code above step-by-step.
- It units preliminary beliefs (priors) for the intercept, slope, and noise.
- It defines a probability perform primarily based on these priors and the noticed knowledge.
- The code makes use of Markov Chain Monte Carlo (MCMC) sampling to generate samples from the posterior distribution.
- Lastly, it summarizes the outcomes to indicate estimated parameter values and uncertainties.
Wrapping Up
Bayesian strategies mix prior beliefs with new proof for knowledgeable decision-making. They enhance predictive accuracy and handle uncertainty in a number of domains. Instruments like PyMC4, Stan, and TensorFlow Chance present sturdy assist for Bayesian evaluation. These instruments assist in making probabilistic predictions from complicated knowledge.
Jayita Gulati is a machine studying fanatic and technical author pushed by her ardour for constructing machine studying fashions. She holds a Grasp’s diploma in Laptop Science from the College of Liverpool.

