How few corners can a form have and nonetheless tile the aircraft?” mathematician Gábor Domokos requested me over pizza. His deceptively easy query was in regards to the geometry of tilings, additionally referred to as tessellations—preparations of shapes, referred to as tiles or cells, that fill a floor with no gaps or overlaps. People have a preoccupation with tessellation that dates again a minimum of to historical Sumer, the place tilings featured prominently in structure and artwork. However in all of the centuries that thinkers have tinkered with tiles, nobody appears to have significantly contemplated whether or not there’s some restrict to how few vertices—sharp corners the place strains meet—the tiles of a tessellation can have. Till Domokos. Chasing tiles with ever fewer corners ultimately led him and his small workforce to find a completely new sort of form.
It was the summer time of 2023 when Domokos and I sat at a wooden picnic desk on the Black Canine, a comfortable spot for pizza and wine only a few blocks from the Budapest College of Expertise and Economics, the place Domokos is a professor. He reached throughout the desk to seize a paper pizza menu and flip it over, revealing a clean underside, and gestured to me to seize a pen. The midsummer sky was taking up shades of orange and indigo as I stuffed the menu with triangles. Domokos watched expectantly. “You’re allowed to use curves,” he lastly mentioned. I began filling the web page with circles, which after all can’t fill area on their very own. However Domokos lit up. “Oh, that’s interesting!” he mentioned. “Keep going, you can mix shapes. Just try to keep the average number of corners as low as possible.”
I stored going. My web page of circles full of more and more determined, squiggly types. Domokos’s pizza Margherita had lengthy since disappeared, however he wasn’t fairly prepared to depart. A fast look at my crude drawing wasn’t sufficient to find out its common variety of corners, not to mention the minimal potential. However the correct reply will need to have been one thing lower than the triangle’s three—in any other case, the query could be boring.
On supporting science journalism
If you happen to’re having fun with this text, think about supporting our award-winning journalism by subscribing. By buying a subscription you’re serving to to make sure the way forward for impactful tales in regards to the discoveries and concepts shaping our world at this time.
That remark appeared to fulfill the mathematician, who revealed that the actual reply is 2. “That’s an easy question,” he mentioned. “But what about 3D?”
“This is a tool that can reasonably describe, at least to me, a wide range of more physically relevant things than just polyhedrons stuck together.” —Chaim Goodman-Strauss, mathematician
Now, greater than a yr after that night on the pizza store, Domokos has the reply. Discovering it was an thrilling, irritating problem that finally led him and three colleagues to find “soft cells,” shapes that may match collectively to utterly fill a flat floor or a three-dimensional area with as few corners as potential. In two dimensions, delicate cells have two corners bridged by curves. However in 3D, these curvy, nearly natural types haven’t any corners in any respect. As soon as the researchers recognized the brand new shapes, they started to see them all over—in nature, artwork and structure. The outcomes have now been revealed within the journal PNAS Nexus.
Though delicate cells hadn’t been categorized by mathematicians earlier than—nobody had observed or named them in an educational paper—they abound in artwork and nature, from the structure of Zaha Hadid, “Queen of the Curve,” to the types of zebra stripes. Krisztina Regős, Domokos’s graduate scholar, discovered the primary pure 3D delicate cell tucked away within the chambers of the nautilus shell, an object that’s change into iconic for showcasing the convergence of math and biology. “They were in front of our eyes the whole time,” Regős says. This connection to such a well-known form led Domokos to worry that his group could be scooped. He swore his collaborators to secrecy till their discovery was able to be revealed. (It got here out in September.) On the finish of his lesson over pizza, he even took the paper menu, folded it up and pocketed it. Simply to be secure.
Looking back, it ought to have been apparent that delicate cells exist, says mathematician Joseph O’Rourke of Smith Faculty, who wasn’t concerned within the examine. However to assume to ask such a query, “to even imagine that you can tile space with no vertices,” he says, is unique. “I found that quite surprising and very clever.”
“This is a tool that can reasonably describe, at least to me, a wide range of more physically relevant things than just polyhedrons stuck together,” says mathematician Chaim Goodman-Strauss of the College of Arkansas, an knowledgeable on tiling. “Just look at the foam in a glass of beer, and you’ll know they’re onto something.”
Years in the past Domokos developed a mathematical software for describing tessellations based mostly on their common properties reasonably than the shapes of particular person cells. The thought grew out of labor on pure mosaics, similar to cracked rock faces. Utilizing averages captures the essence of the tessellation with out imposing unnatural rigidity.
As Domokos and Regős explored the foundations governing the common properties of mosaics, they realized one thing: it didn’t appear potential to get the common variety of vertices (corners) per tile beneath two. From there it wasn’t a lot of a leap to appreciate {that a} monotile—a tile that fills the aircraft solely with copies of itself, such because the common hexagons of a honeycomb or squares of a checkerboard—couldn’t have fewer than two vertices. This rule hadn’t been acknowledged earlier than.
When Domokos and Regős couldn’t discover any earlier work on the topic, the duo realized that they had one thing attention-grabbing on their fingers. However they felt out of their geometric depth when it got here to translating their discovery into a proper mathematical rule. They recruited geometer Ákos G. Horváth, who additionally works on the Budapest College of Expertise and Economics, to their trigger.
Horváth quickly devised an algorithm that would warp polygonal tilings of the aircraft into tilings of shapes with simply two vertices. Utilizing it, the workforce devised rounded, delicate, two-vertex tiles from common tilings of triangles, hexagons and rectangles. The hexagonal tiles they used appear to be hexagons which have had two corners stretched out and the remainder floor all the way down to rounded nubs. The square-derived tiles are extra various. One appears to be like like a deformed sq., however the others resemble shingles, fish scales, lentils and the flukes of whales. The 2 forms of tiles derived from triangles look a bit like a hill and a ship’s sail.
Then, Domokos says, “we started to fantasize about what it is in 3D.”
Jen Christiansen; Supply: “Soft Cells and the Geometry of Seashells,” by Gábor Domokos, Alain Goriely, Ákos G. Horváth and Krisztina Regős; February 6, 2024; arXiv:2402.04190 (tile reference)
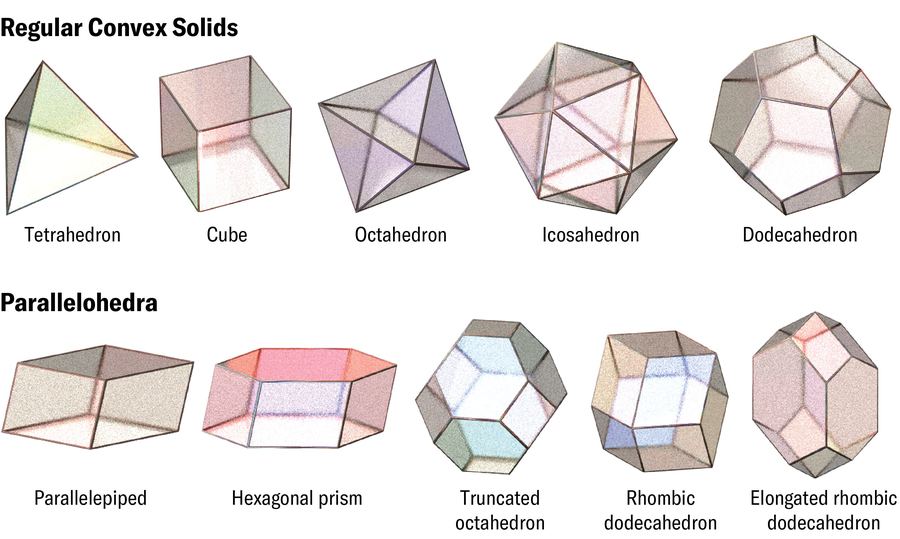
Folks have been imagining 3D tessellations a minimum of since Plato’s time. He constructed his mannequin of the universe round tessellations of the 5 common convex solids: tetrahedron, dice, octahedron, icosahedron and dodecahedron. Tessellations of the primary 4 shapes ought to construct the classical components of earth, air, water and hearth, respectively, Plato figured. The dodecahedron was the stuff of the cosmos. Plato was incorrect about greater than this esoteric cosmology. Solely the dice can really fill 3D area as a monotile—with actual copies of 1 form—with out gaps and overlaps (except the area itself is curved). However cubes squished and stretched into parallelepipeds (shapes with six parallelograms for faces) can fill area, too. And in 1885 Russian crystallographer Evgraf Fedorov cataloged a set of 5 shapes referred to as the parallelohedra—3D types that may be packed collectively with none rotation. These shapes embrace the dice and the hexagonal prism acquainted from honeycombs, in addition to the extra esoteric rhombic dodecahedron, elongated dodecahedron and truncated octahedron.
All these shapes are polyhedra with flat faces and straight edges. However 3D shapes with curves can fill area, too—though the prepared examples are solely barely bent and have apparent corners. Tellingly, the recognized examples all emerged from questions on nature, not summary arithmetic. In 1887 British mathematician William Thomson, also called Lord Kelvin, posed a puzzle: What association of cells or bubbles of equal quantity minimizes the floor space of the interfaces between them? In different phrases, what’s the optimum foam?
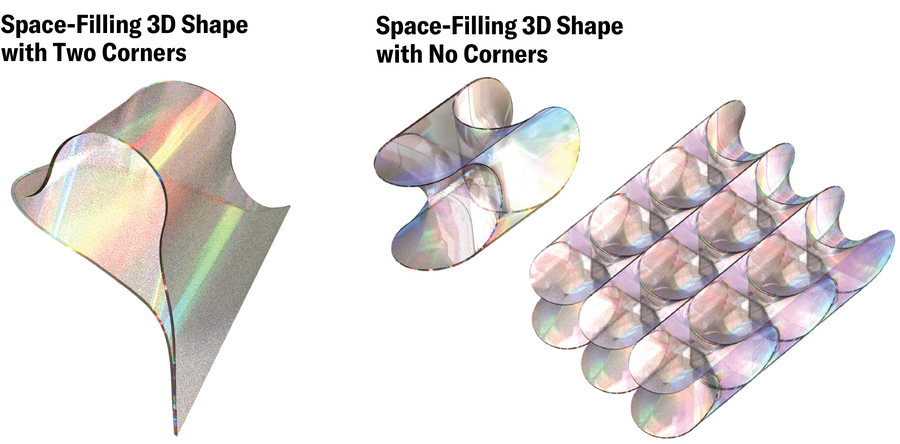
Kelvin’s first resolution was a tessellation of barely warped truncated octahedra. In a 1994 paper, physicists Denis Weaire and Robert Phelan, each then at Trinity Faculty Dublin, beat Kelvin’s construction with a tessellation of two completely different warped polyhedra. And in 2018 a workforce of biophysicists led by Luis M. Escudero of the College of Seville and Javier Buceta of the Institute for Integrative Techniques Biology in Spain found a brand new form referred to as a scutoid, resembling a warped honeycomb, which the physique’s epithelial cells assume to pack optimally in tissues that have to bend and curve. Nonetheless, nobody appears to have requested how few corners a space-filling strong can have. The Hungarian workforce’s leap to 3D was, at first, a leap of religion. “We had not the faintest idea. Not even a hunch,” Domokos says.

When the trio ultimately recognized a space-filling 3D form with simply two corners, Domokos thought they’d discovered their reply. “I got completely obsessed with this whole thing,” he says. “And I wrote a paper proving that the minimum number [of corners] in three dimensions is two.” The proof grew out of a easy assumption that Domokos thought was trivial. However as months got here and went, he slowly began to appreciate that the idea wasn’t so minor in spite of everything—and it’d even be incorrect. “He wanted to send this article to me and Ákos for Christmas. Then for New Year’s Eve. And then later and later,” Regős remembers, combating again a smile. “And then he found an example with zero. So that was that.” The form was itself a proof: in three dimensions, it’s potential to tessellate area with objects that haven’t any corners in any respect.
Violet Frances; Supply: “Soft Cells and the Geometry of Seashells,” by Gábor Domokos, Alain Goriely, Ákos G. Horváth and Krisztina Regős; February 6, 2024; arXiv:2402.04190 (reference)
Discovering that first delicate cell answered one query and opened up numerous extra. The researchers questioned, as an illustration, whether or not space-filling shapes with precisely one nook might exist. Domokos ultimately discovered one. When he sketched it out on a blackboard for Regős and Horváth, they had been “disgusted,” he says. It was an unsightly form—a warped type with no symmetries that appears like one thing dreamed up by an alien. However someplace in that ugliness, Regős glimpsed risk. “I just saw it one day and realized,” she says. “We can do this edge-bending thing and create the softness.”
Regős’s instinct was that she might create delicate cells by bending the sides of regular, pointed polyhedra. At every vertex the place three edges met, she’d seize two edges and coerce them into curves that ran parallel to the remaining edge the place the vertex was earlier than. A closed strong in 3D area should enclose 4π levels of curvature, that are normally concentrated at vertices. Regős was smearing out that curvature over edges as a substitute. “It took days and days and days to convince me that what she’s doing is not completely rubbish,” Domokos says.
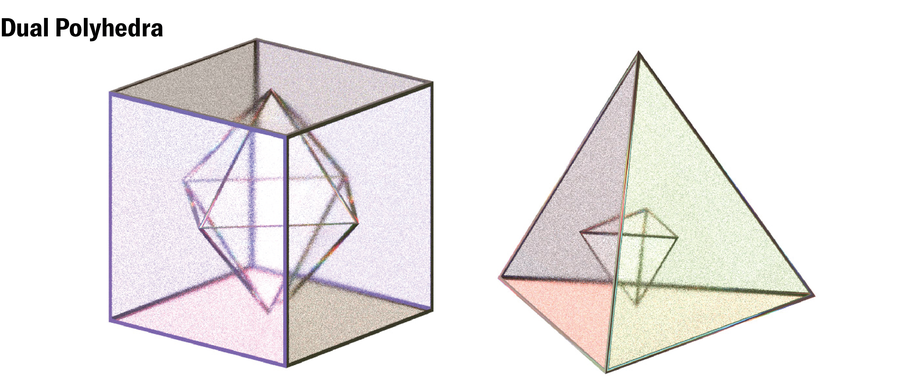
Regős had bother describing her methodology for bending edges in mathematical language. However then she realized the method might be boiled all the way down to an simply solved 2D downside from graph idea. Each polyhedron has a twin—one other polyhedron whose faces correspond to its edges and vice versa. The workforce confirmed that if it’s potential to discover a path alongside the sides of a polyhedron’s twin that visits every of its vertices precisely as soon as—what’s referred to as a Hamiltonian circuit—it’s additionally potential to warp that form right into a cornerless, space-filling delicate cell.
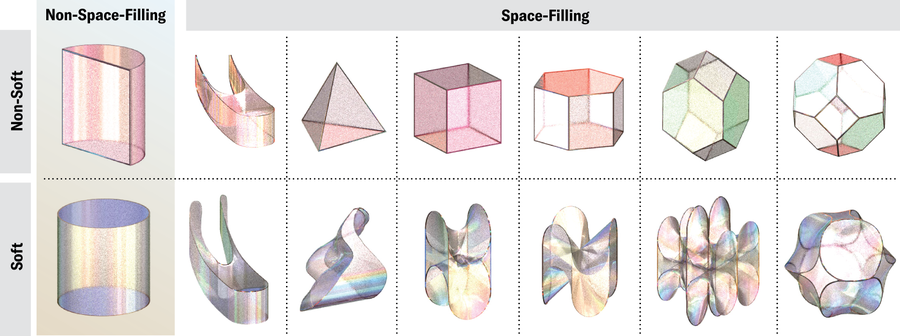
With that situation set, Horváth might lastly write a mathematical 3D edge-bending algorithm. By mapping an infinite class of polyhedral tilings to delicate tilings, he proved the existence of an infinite class of soppy cells. In different phrases, for each polyhedron—a 3D form with flat polygonal faces—that would fill area with itself, there should even be a curved delicate cell.
To O’Rourke, the edge-bending algorithm is essentially the most stunning and vital a part of the paper. The magnificence comes from uniting two fully completely different fields of arithmetic. Hamiltonian circuits are purely combinatorial (having to do with the arithmetic of counting)—they’ve “nothing to do with geometry,” O’Rourke explains. “But here you’re very much in geometry. And yet you need this combinatorial condition. So I find that very nice.”
Violet Frances; Supply: “Soft Cells and the Geometry of Seashells,” by Gábor Domokos, Alain Goriely, Ákos G. Horváth and Krisztina Regős; February 6, 2024; arXiv:2402.04190 (reference)
As they got here to grasp the arithmetic of 2D delicate cells, the mathematicians started to appreciate that the shapes existed past their sketches and notes. “They were right under our noses,” Domokos says. The workforce began to see planar mosaics of two-vertex tiles all over the place, from muscle tissue to zebra stripes. As soon as, on a stroll by means of Budapest, Regős even noticed them within the curvy crisscross of a metallic security grate.
On the identical time, the trio was discovering increasingly more 3D delicate cells—Regős added warped variations of 4 parallelohedra, in addition to tetrahedra, to Domokos’s first form, a warped dice. However the researchers struggled to determine these 3D delicate cells in the actual world. That modified when, a couple of yr after Domokos first discovered the edge-bent dice, he realized he’d seen it someplace earlier than—not in nature however in structure.
A few decade earlier, architect Viki Sándor and a bunch of scholars on the College of Vienna had concocted an uncommon design for a Cirque du Soleil efficiency heart. The constructing was by no means constructed, nevertheless it bought some consideration in architectural circles. Its basic constructing block was a form that appears nearly precisely like Domokos’s cubic delicate cell.
Sándor’s undertaking began as a warm-up train across the theme of “balance,” says the architect, now on the Austrian Institute of Expertise. The constructing needed to be modular, so that they divided it into cubic blocks, every to be designed by a distinct individual. By coincidence, the design was impressed by a self-balancing form referred to as the gömböc, found in 2006 by Domokos and structural mechanics researcher Péter Várkonyi. Sándor and her teammates appreciated the gömböc’s distinction of thinness and fatness and wished an identical form that may match completely different modules collectively. They discovered their reply within the C-shaped curves of a tennis ball. “If you cut along the C-shape, then you get a very thin and a very fat element. And the gömböc follows this principle,” Sándor says. Slicing curved surfaces into tubes or prisms turned out to be methodology for developing delicate cells—not simply in idea or design but additionally in nature.
Regős discovered the primary pure 3D delicate cell in a flash of instinct. In the future out of the blue she e-mailed Domokos an image of a cross part of a nautilus shell. Domokos replied that it was a pleasant instance of 2D delicate cells. Regős wrote again: no, they had been 3D delicate cells. “It doesn’t look soft at all,” Domokos thought. “I mean, it has corners.” However Regős was insistent. So Domokos purchased two nautilus shells and introduced them to Regős and Horváth for inspection. They performed with the shells for half-hour or so earlier than giving up. Even when they might persuade themselves simply by trying on the shells, Domokos says, “you cannot send in a shell to a paper as an attachment.”
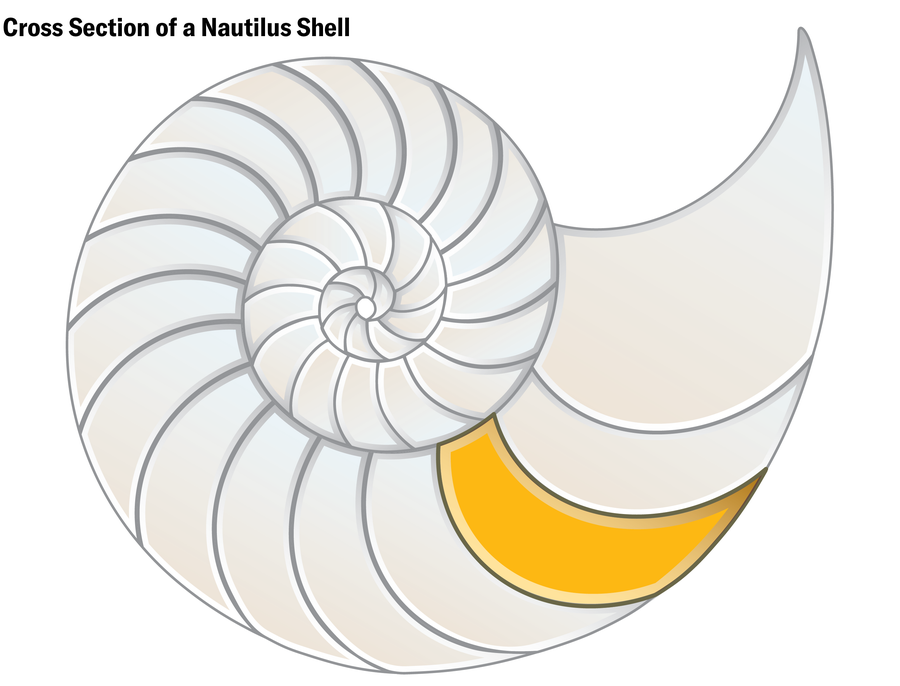
Jen Christiansen; Supply: “Soft Cells and the Geometry of Seashells,” by Gábor Domokos, Alain Goriely, Ákos G. Horváth and Krisztina Regős; February 6, 2024; arXiv:2402.04190 (reference)
The thought may need died there if not for a freely obtainable set of micro CT scans revealed by the D’Arcy Thompson Zoology Museum on the College of Dundee in Scotland. Domokos discovered the scans on-line and spent hours “crawling around inside” the shells, on the lookout for corners. He couldn’t discover any.
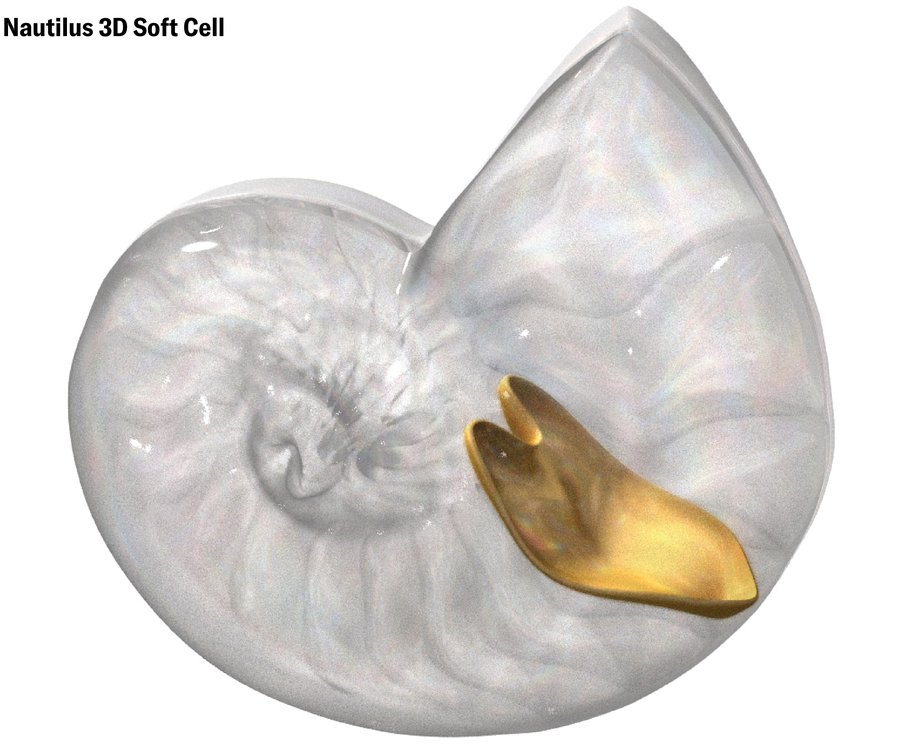
Violet Frances; Supply: “Soft Cells and the Geometry of Seashells,” by Gábor Domokos, Alain Goriely, Ákos G. Horváth and Krisztina Regős; February 6, 2024; arXiv:2402.04190 (reference)
Nobody on the workforce knew the very first thing about shells. However Domokos knew somebody who did: Alain Goriely, a physicist and utilized mathematician on the College of Oxford who had studied chambered seashells. Domokos was nervous to inform anybody outdoors his small group in regards to the undertaking, particularly now that they’d found delicate cells contained in the nautilus shell—a favourite type amongst mathematicians keen on pure shapes. It might have been simple to scoop their thought and publish it first. However Domokos had recognized Goriely for many years, so he determined to take a threat and name him. Not lengthy after, he and Regős had been on a aircraft headed for Oxford.
Goriely was instantly gripped by the invention of soppy cells throughout the nautilus shell. “I find it is quite natural for shapes in nature to go that way because forming sharp corners is very costly,” Goriely says. Organic cells are delicate, and floor rigidity will naturally spherical them off except the organism expends vitality to construct inflexible buildings that may maintain pointier shapes. And cells inside a dwelling factor need to fill area effectively with few gaps.
Of their three frantic days at Oxford and the months that adopted, Goriely and the Hungarians recognized increasingly more examples of soppy cells in nature and artwork. Zebra stripes, river estuaries, cross sections of onions, seashells, heads of wheat, crimson blood cells, vegetation and fungi all resembled 2D delicate cells. And in structure, 2D delicate cells lend futuristic, natural types to many buildings by architect Zaha Hadid. Additionally they seem in sketches of tatami and clothes by Japanese artist Katsushika Hokusai, who made the well-known 1831 portray The Nice Wave off Kanagawa, in addition to within the artwork of Victor Vasarely, the “grandfather” of the optical artwork motion.
Goriely helped the workforce discover one other instance of 3D delicate cells, too: the chambers of ammonite shells. Then Regős concocted a geometrical mannequin that produces shapes much like the seashell examples from first ideas. Mushy cells like these within the nautilus shell are simply made by intersecting a prism with curved surfaces—an echo of the method Sándor and her workforce used to design the Cirque du Soleil constructing. “What’s nice is that architects have intuitively reached that [process] also,” Goriely says. “From our understanding, they’ve reached it with the same types of requirements: they wanted to soften the structure.”
The work establishes a “useful vocabulary” for exploring delicate shapes, Goodman-Strauss says—a vocabulary that opens up new mathematical questions. What classes of soppy monotiles exist? What teams of soppy shapes can and can’t tile area? Domokos wonders how softness pertains to aperiodicity, the flexibility to tile a aircraft with out making a repeating sample. The invention of the primary aperiodic monotiles—single shapes that fill area with solely copies of themselves however by no means repeat a sample—made headlines final yr. Domokos and Regős had been inquisitive about what would occur in the event that they utilized their edge-softening algorithm to the “spectre” tiling, the primary actually aperiodic monotile. However they had been shocked to find that its softened model couldn’t tile a aircraft alone.

Jen Christiansen; Supply: “A Chiral Aperiodic Monotile,” by David Smith, Joseph Samuel Myers, Craig S. Kaplan and Chaim Goodman-Strauss; Could 28, 2023; arXiv:2305.17743 (reference)
Arkansas’s Goodman-Strauss and Craig S. Kaplan of the College of Waterloo in Ontario, who each contributed to the invention of the primary aperiodic monotiles, didn’t discover it shocking in any respect. Mathematicians are simply beginning to discover aperiodic monotiles, and there are various questions left to reply, Kaplan says.
Regardless of the seeming ubiquity of soppy cells in nature, the hyperlink between the arithmetic of those shapes and biology is, for now, only a visible remark. Domokos admits that this can be a weak level of the work and wish to set up the explanations they’re so widespread in nature. “A lot of the paper is about visual similarity, and that’s very unusual,” he says. Exploring this hyperlink additional seems promising, although, Kaplan says. “I do like the motivation: just the simple claim that nature doesn’t like sharp features, so let’s investigate that from a mathematical perspective. It’s a nice opening gambit from which you can develop a rich theory.”
And the idea of soppy cells might grow to be helpful down the road, Goodman-Strauss says—“not necessarily to the biologists of today but the biologists 30 years from now.” Maybe the arithmetic of soppy cells will finally seize one thing actual about delicate matter—the malleable supplies that make up most of our world, from the blood in our veins to the liquid-crystal show you could be studying on proper now.
Questions on delicate geometry are significantly tough to check as a result of they have an inclination to defy disciplinary boundaries. Domokos struggled for months to discover a journal that may publish the workforce’s “outlandish” manuscript mixing math, artwork and biology. That’s not shocking to Goodman-Strauss. Requested the place he thinks delicate cells belong within the scientific panorama, he doesn’t skip a beat. “I think,” he says, “the only answer is it belongs to the future.”

